Introduction

Wordle, as you know, is the new Internet rage. It is a simple word puzzle game, where you have to guess a 5 letter word in 6 tries

What I wanted to do

I wanted to do something with the stats of the game, particularly the Guess Distribution. I wanted to build a tool which calculates some properties of this distribution.

This was something I enjoyed building. It's Fun!

How the code works

The number of guesses can be between 1 and 6 (both inclusive), so we use an array to store the frequencies of those guess numbers corresponding to the actual guess number. For example, f[1] = number of 1 guess wins, f[2] = number of 2 guess wins, and so on.

The formula for calculating mean:

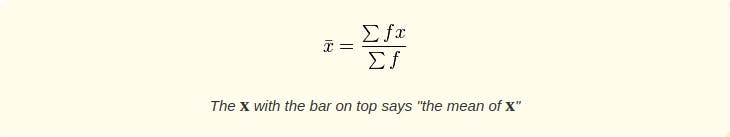where f is the frequency and x is the number of guesses

We use this bit of code to compute it

for(int i = 1; i <= 6; i++)
{
    printf("How many %d guess wins?\n", i);
    scanf("%d", &f[i]);
    s1 += i*f[i];
    n += f[i];
}

float m1 = s1/n;

We also calculate the second, third and fourth order central moments like this

// calculate 2nd, 3rd and 4th order central moments
for(int j = 1; j <= 6; j++)
{
    s2 += pow((j - m1), 2)*f[j];
    s3 += pow((j - m1), 3)*f[j];
    s4 += pow((j - m1), 4)*f[j];
}

float m2 = s2/n;
float m3 = s3/n;
float m4 = s4/n;

Variance is the second order central moment, we use the third and fourth order central moments to calculate skewness and kurtosis

float g1 = m3/pow(m2, 1.5); // skewness
float g2 = m4/pow(m2, 2) - 3; // kurtosis

Finally we check the nature of the data from the skewness and kurtosis values

Conclusion

I went with the arithmetic mean, variance, skewness and kurtosis, but it is definitely possible to include many more parameters here.

You can find the full code here

GitHub Repo

Thank you